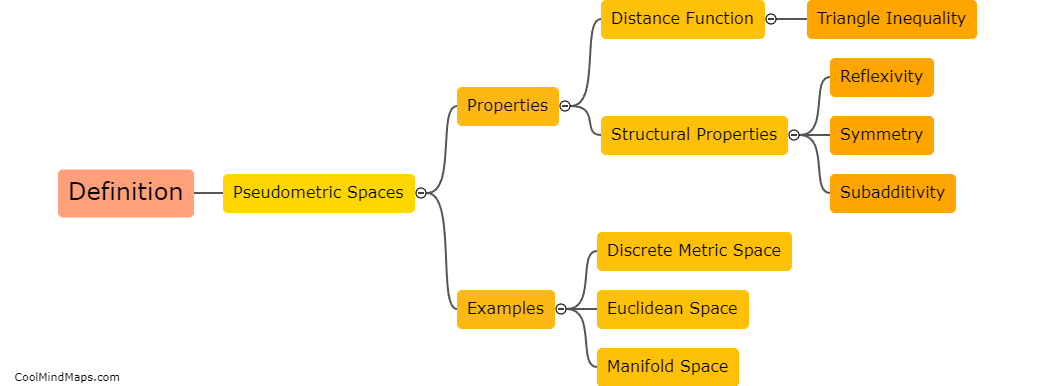
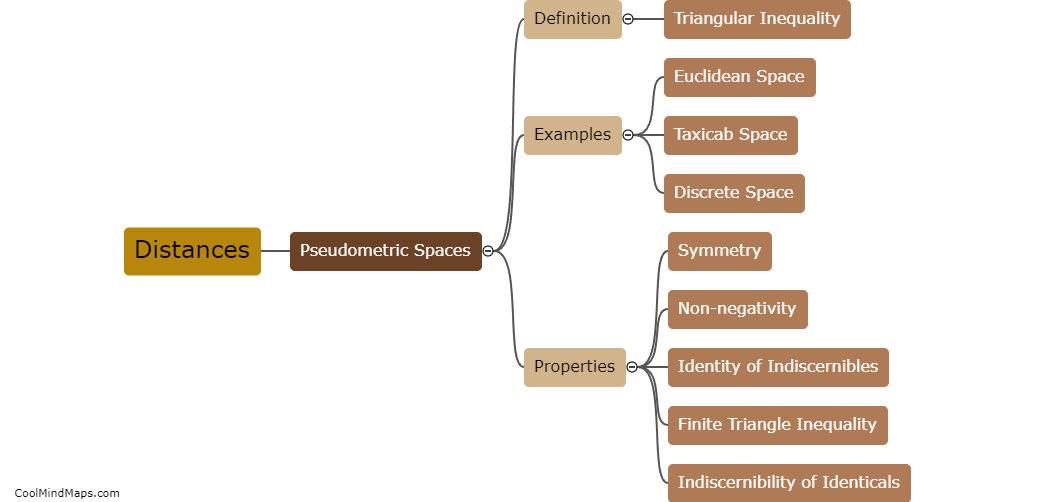
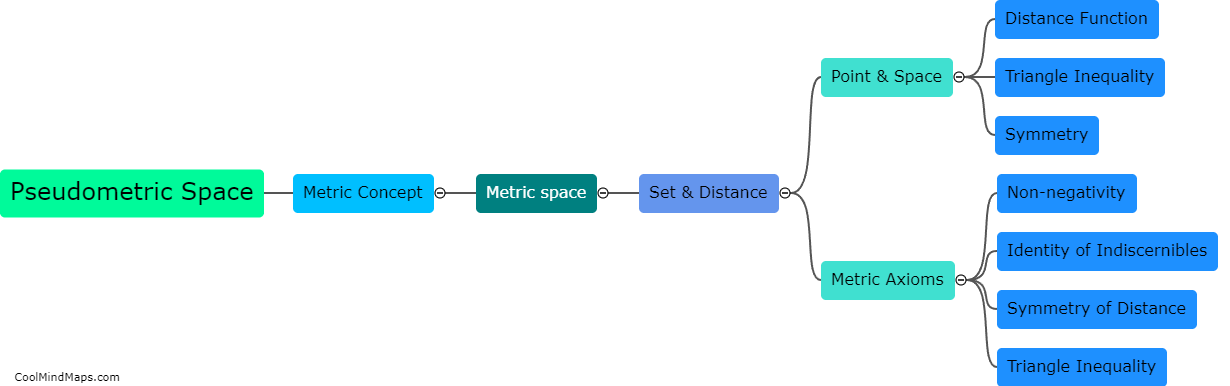
What are the properties of a pseudometric space?

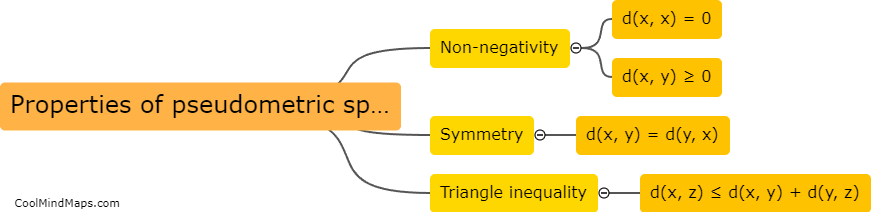
A pseudometric space is a generalization of a metric space, where the concept of distance is relaxed to satisfy slightly weaker conditions. In a pseudometric space, the distance function between two points is allowed to take on the value of zero even if the two points are not the same. Furthermore, the distance function may not satisfy the symmetry property (d(x, y) = d(y, x)), nor the triangle inequality (d(x, z) ≤ d(x, y) + d(y, z)) that is typically expected in a metric space. However, pseudometric spaces do retain some important properties, such as non-negativity (d(x, y) ≥ 0 for all x and y), and the property that the distance between two distinct points is positive if and only if they are not equal.

This mind map was published on 16 November 2023 and has been viewed 96 times.