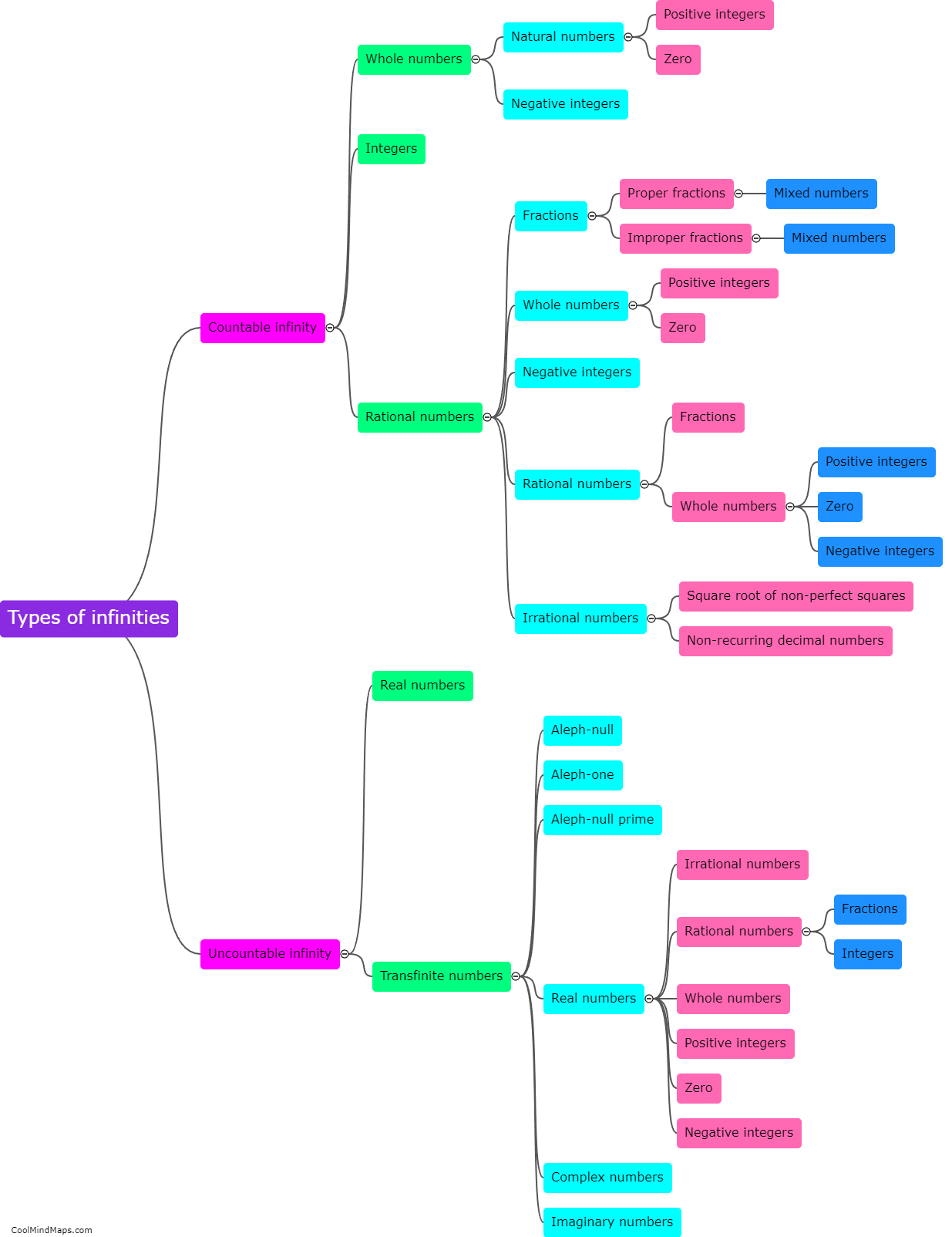
Why are there different sizes of infinities?

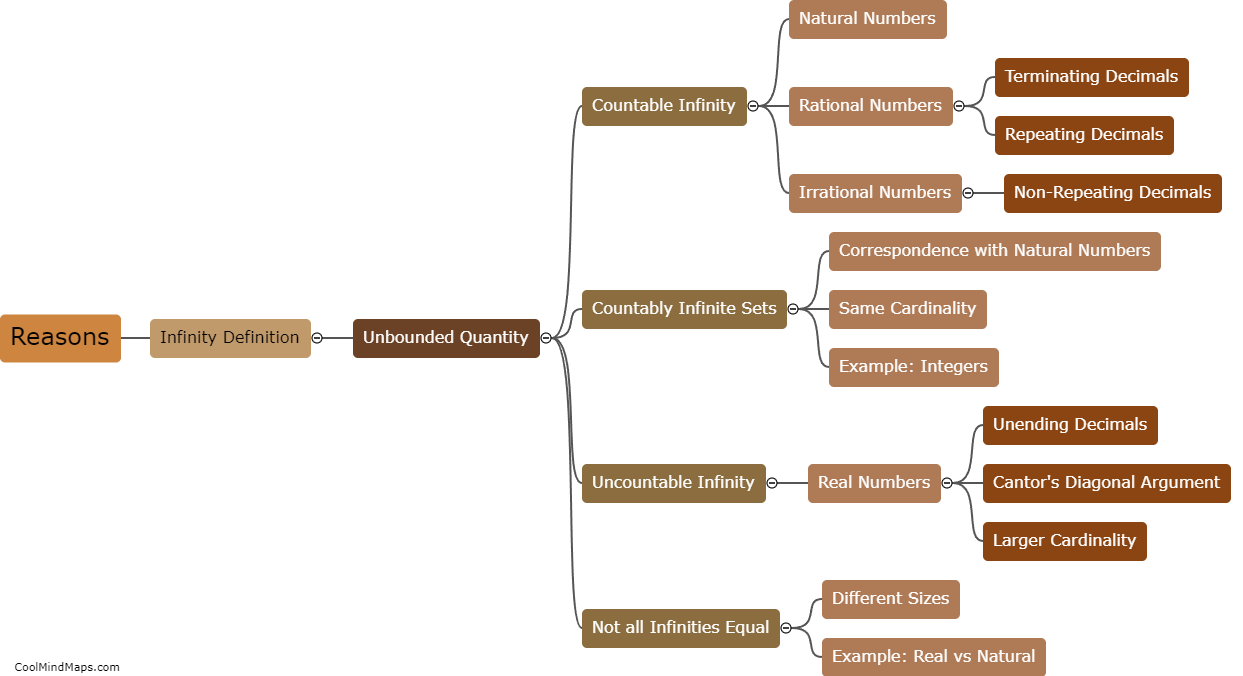
The concept of different sizes of infinities is a fascinating idea in mathematics that arises from Georg Cantor's groundbreaking work on set theory. While the concept may seem counterintuitive, it can be explained through the notion of cardinality, which represents the size or quantity of elements in a set. Cantor showed that not all infinities are equal, as there are infinite sets that have different sizes. He developed a system of comparing the sizes of infinite sets by defining their cardinality using bijections, which are one-to-one correspondences between sets. Through this approach, Cantor established that some infinite sets, such as the set of natural numbers, are smaller than others, like the set of real numbers. This idea challenges our intuitive understanding of infinity but allows mathematicians to explore the rich and diverse nature of the limitless realm of numbers.

This mind map was published on 27 November 2023 and has been viewed 93 times.