What are the basic concepts in Riemannian geometry?

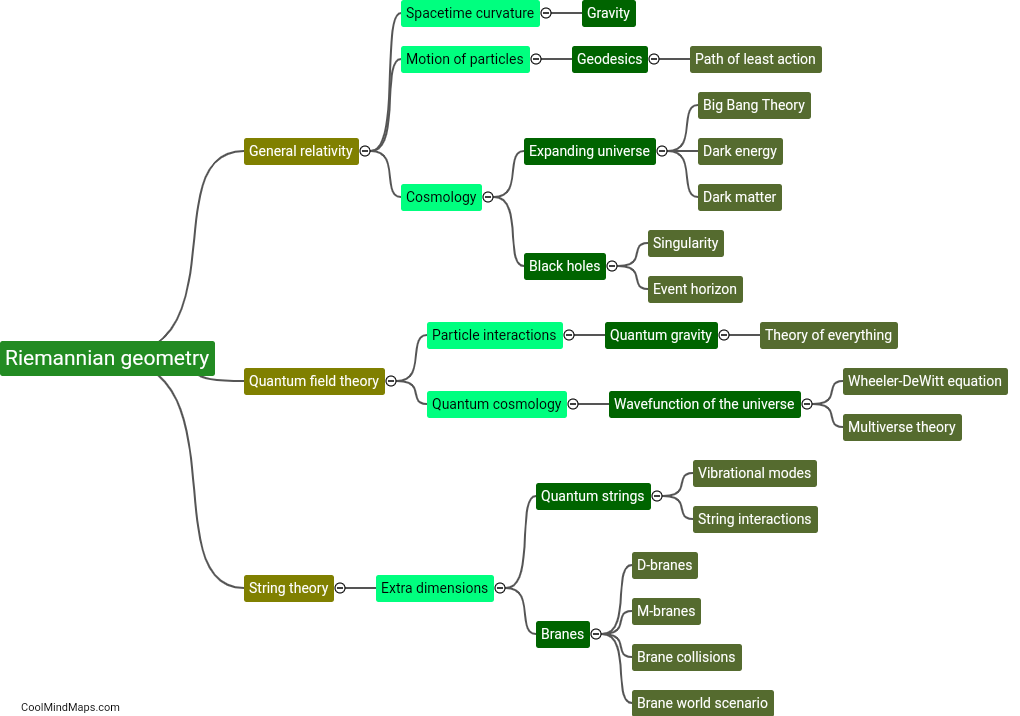
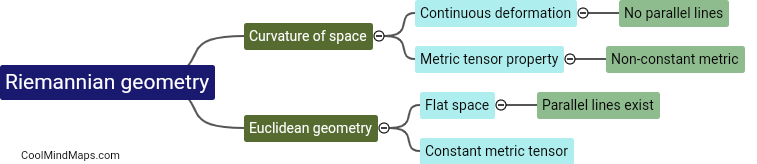
Riemannian geometry is a branch of mathematics that studies curved spaces, in which distances and angles are defined differently than in flat Euclidean spaces. It is based on the work of Bernhard Riemann and involves several fundamental concepts. The most basic concept in Riemannian geometry is the metric tensor, which quantifies how distances change as one moves in various directions on a curved surface. Another key concept is the Riemann curvature tensor, which measures how the curvature of a space varies from point to point. Geodesics, which are the shortest paths between two points, also play a crucial role in Riemannian geometry. Additionally, Riemannian manifolds, which are spaces that locally resemble Euclidean spaces, are studied extensively in this field. These basic concepts form the foundation for exploring more intricate properties and applications of Riemannian geometry in fields such as general relativity and differential geometry.

This mind map was published on 18 September 2023 and has been viewed 83 times.