How can teachers effectively integrate AI tools into their K12 computer science lessons?

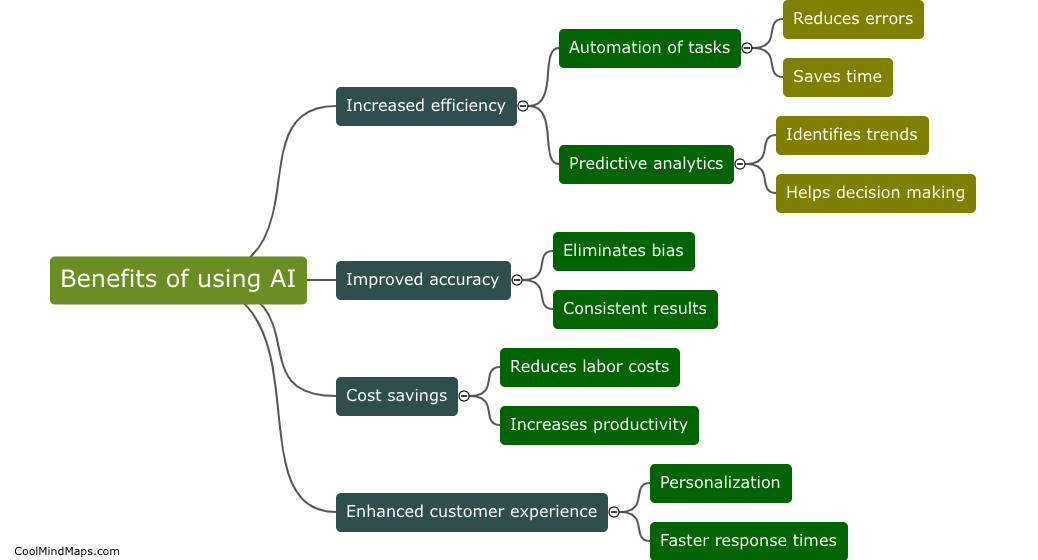
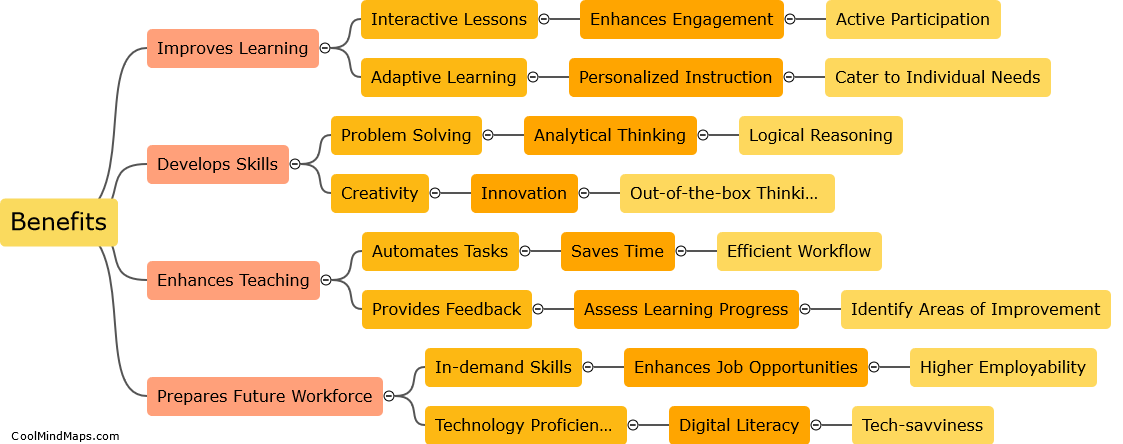
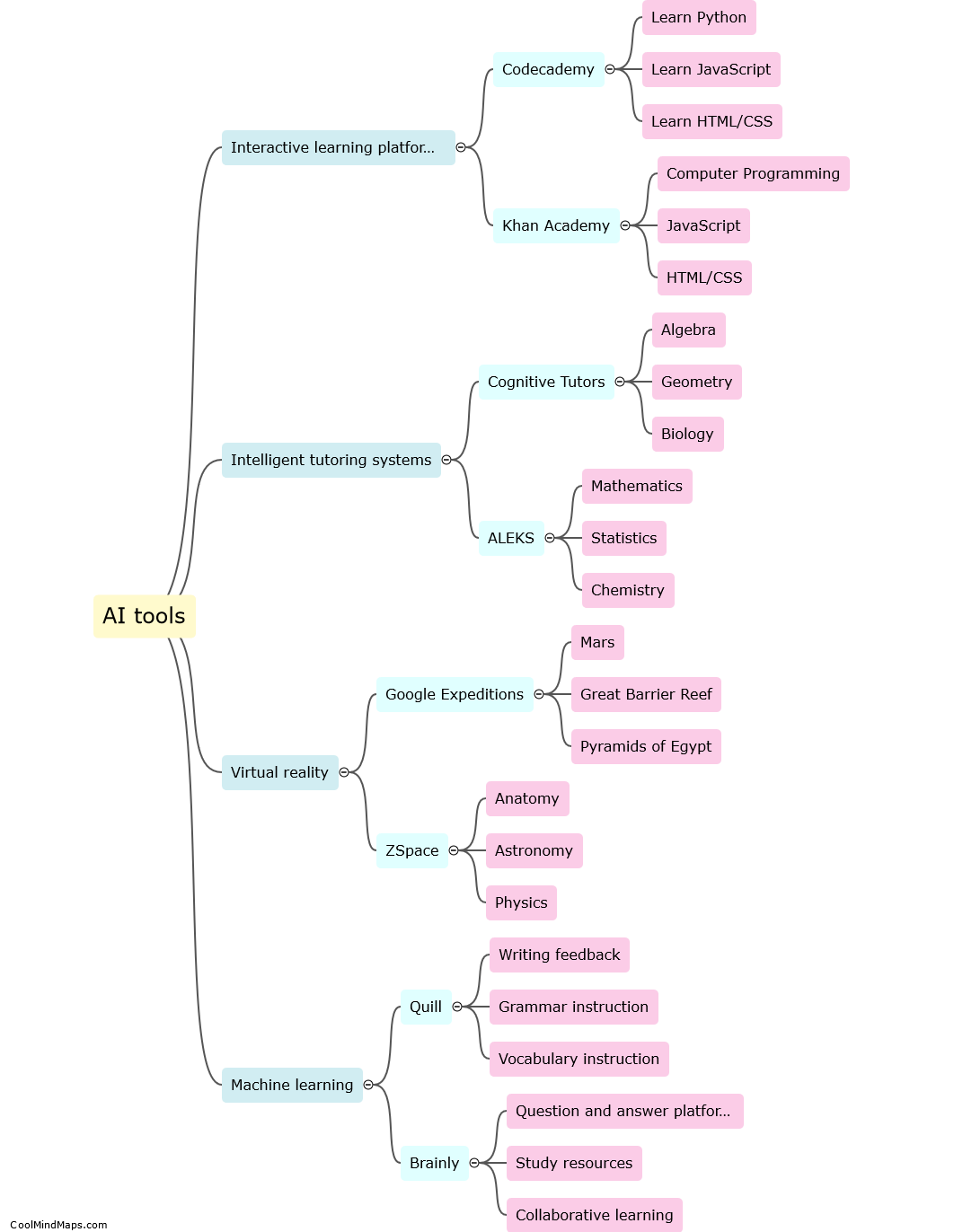
Teachers can effectively integrate AI tools into their K12 computer science lessons by first familiarizing themselves with the available AI resources and understanding their potential applications in the classroom. They should then identify specific learning objectives or lesson topics where AI tools can enhance student engagement and understanding. Next, teachers should select appropriate AI tools that align with their curriculum and instructional goals, ensuring that the tools are age-appropriate and user-friendly. It is important for teachers to provide clear instructions and guidance to students on how to effectively utilize the AI tools, fostering an environment where students can actively explore, experiment, and learn. Additionally, incorporating AI tools into collaborative projects or group activities can encourage teamwork and critical thinking skills. Continuous reflection and assessment should be carried out to evaluate the effectiveness of integrating AI tools, allowing teachers to refine their approach and adjust their instruction accordingly. By integrating AI tools thoughtfully and purposefully, K12 computer science teachers can create engaging and innovative learning experiences that prepare students for the AI-infused world.

AI Tools Teachers Computer Science Lessons K12 Education Integration