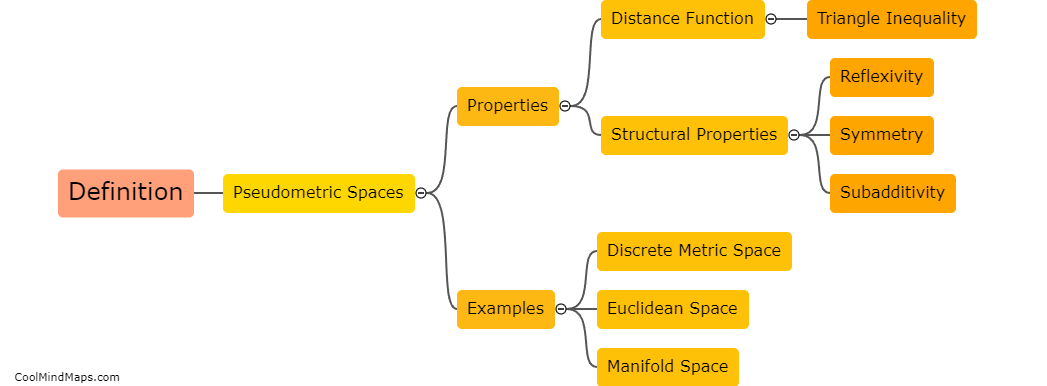
How are distances defined in pseudometric spaces?

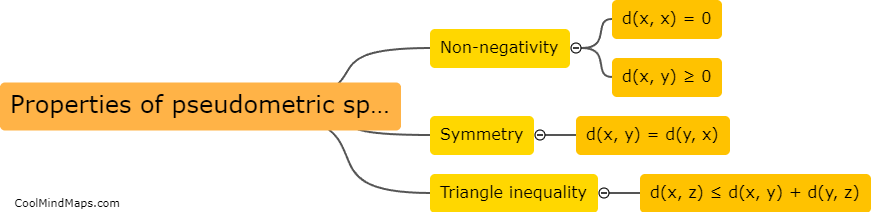
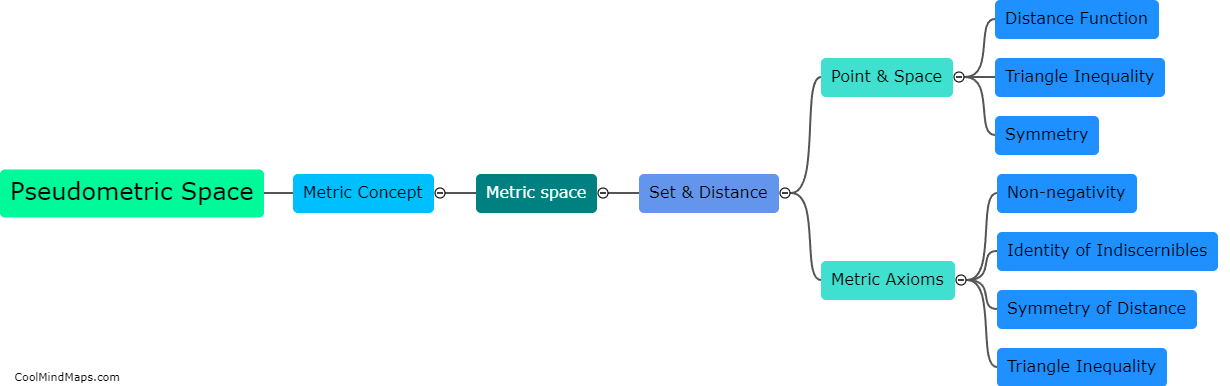
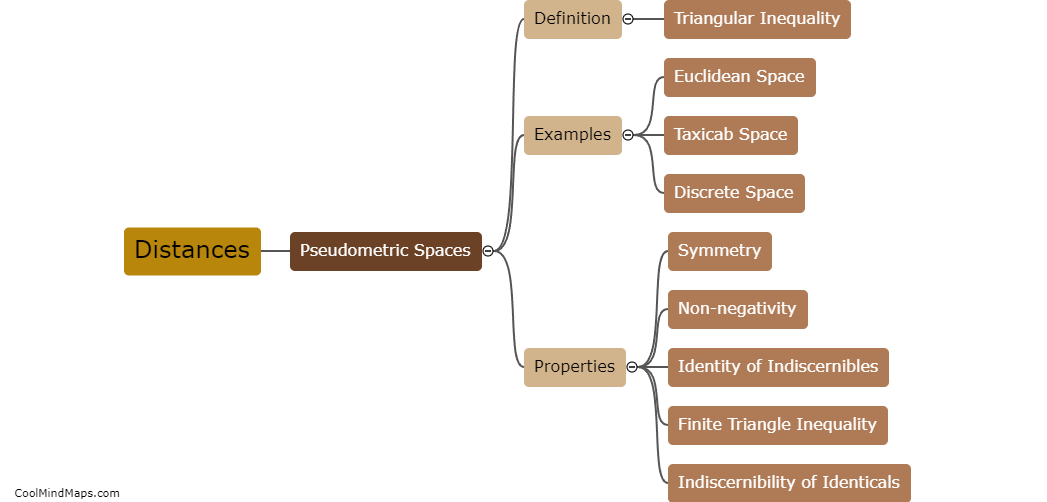
In pseudometric spaces, the concept of distance is defined slightly differently compared to metric spaces. While metric spaces adhere to the triangle inequality property, pseudometric spaces relax this condition. Distances in pseudometric spaces are defined as non-negative real numbers that satisfy the symmetry and positivity properties. Symmetry implies that the distance between two elements is the same, regardless of their order, while positivity ensures that the distance between two distinct points is always greater than zero. The absence of the triangle inequality allows for the possibility of non-unique shortest paths between points, making pseudometric spaces more flexible and applicable in certain mathematical models and theories.

This mind map was published on 10 November 2023 and has been viewed 122 times.