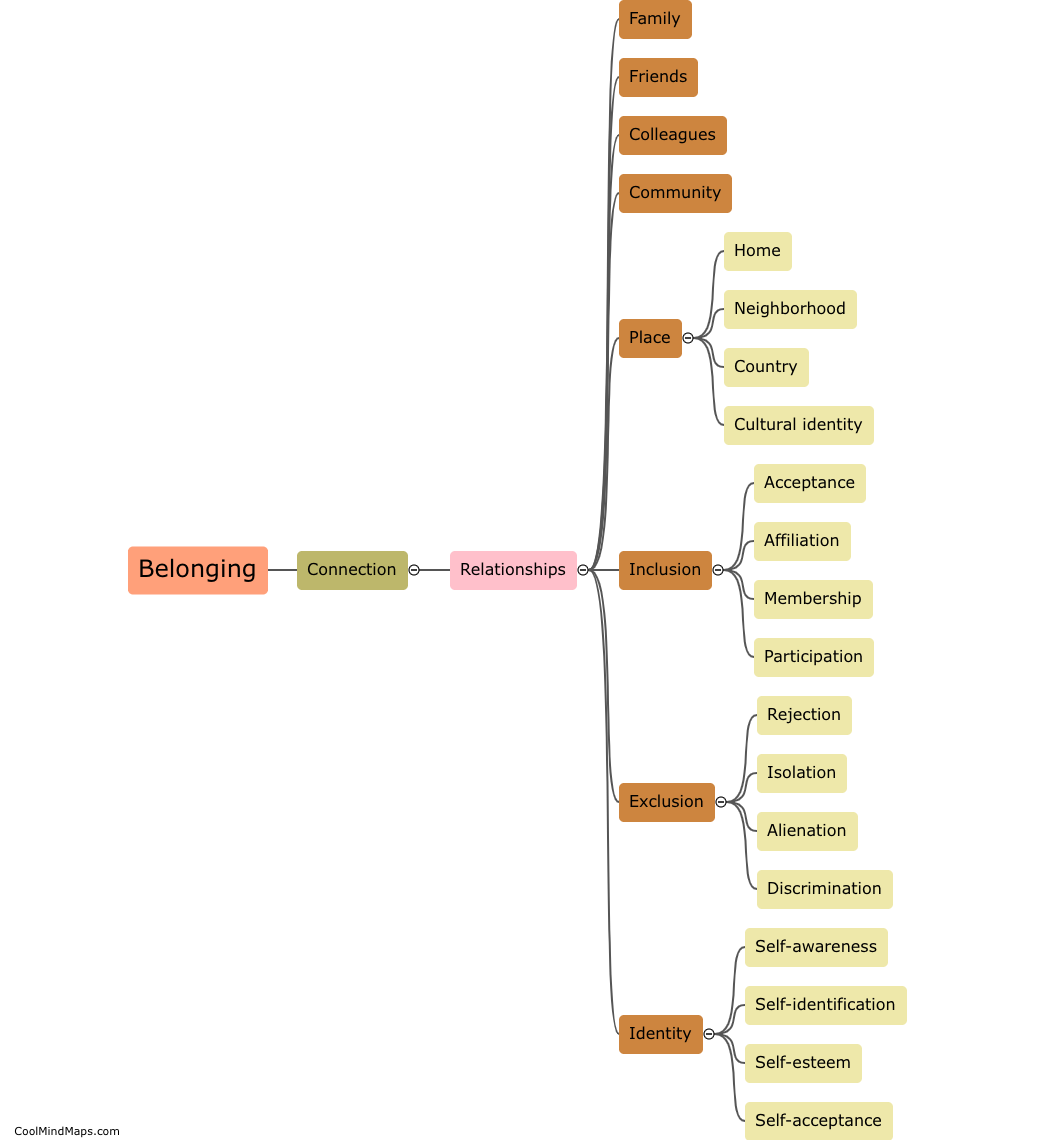
What is a pseudometric space?

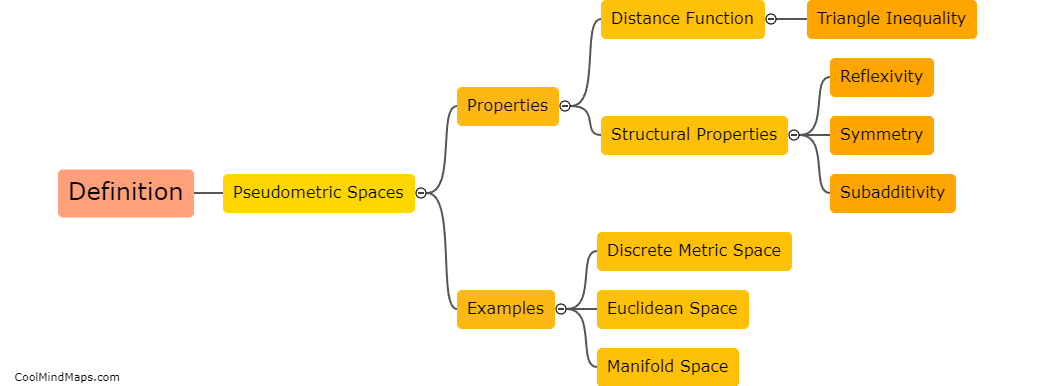
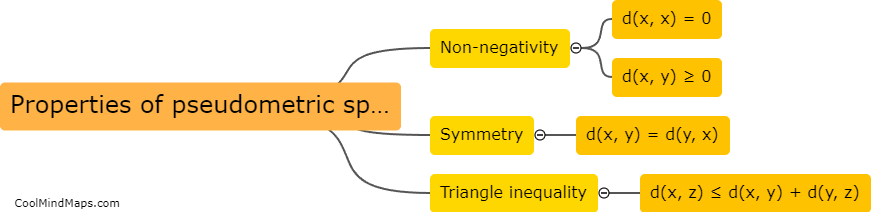
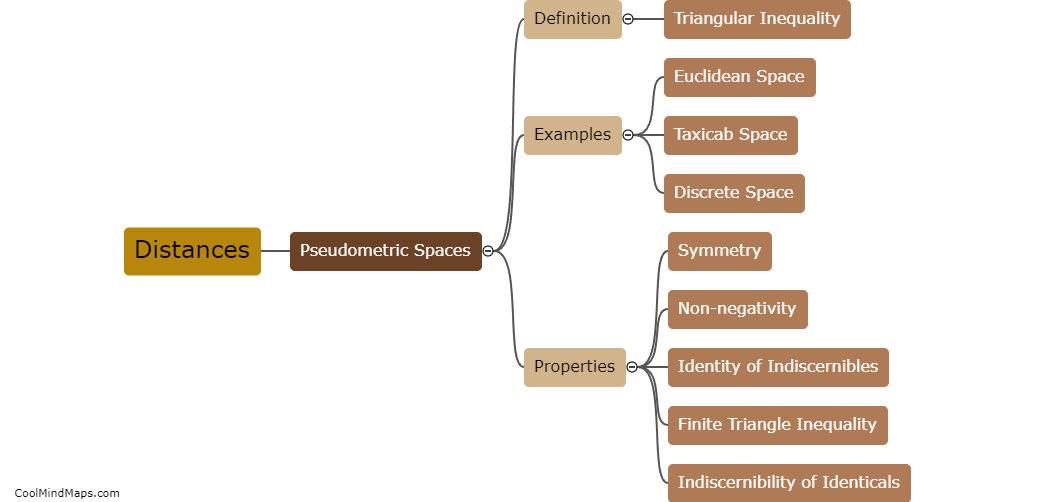
A pseudometric space is a mathematical concept that generalizes the notion of distance in a metric space. While in a metric space, the distance between two points is always non-negative, zero if and only if the points are the same, and satisfies the triangle inequality, a pseudometric space relaxes these conditions. In a pseudometric space, the distance between two points can be zero even if the points are distinct. Furthermore, the triangle inequality may not hold strictly, meaning the sum of two distances can be smaller or equal to the distance between the two points. Pseudometric spaces are useful in various areas of mathematics, such as analysis, topology, and functional analysis, as they provide a more flexible framework to study proximity and convergence.

This mind map was published on 16 November 2023 and has been viewed 96 times.