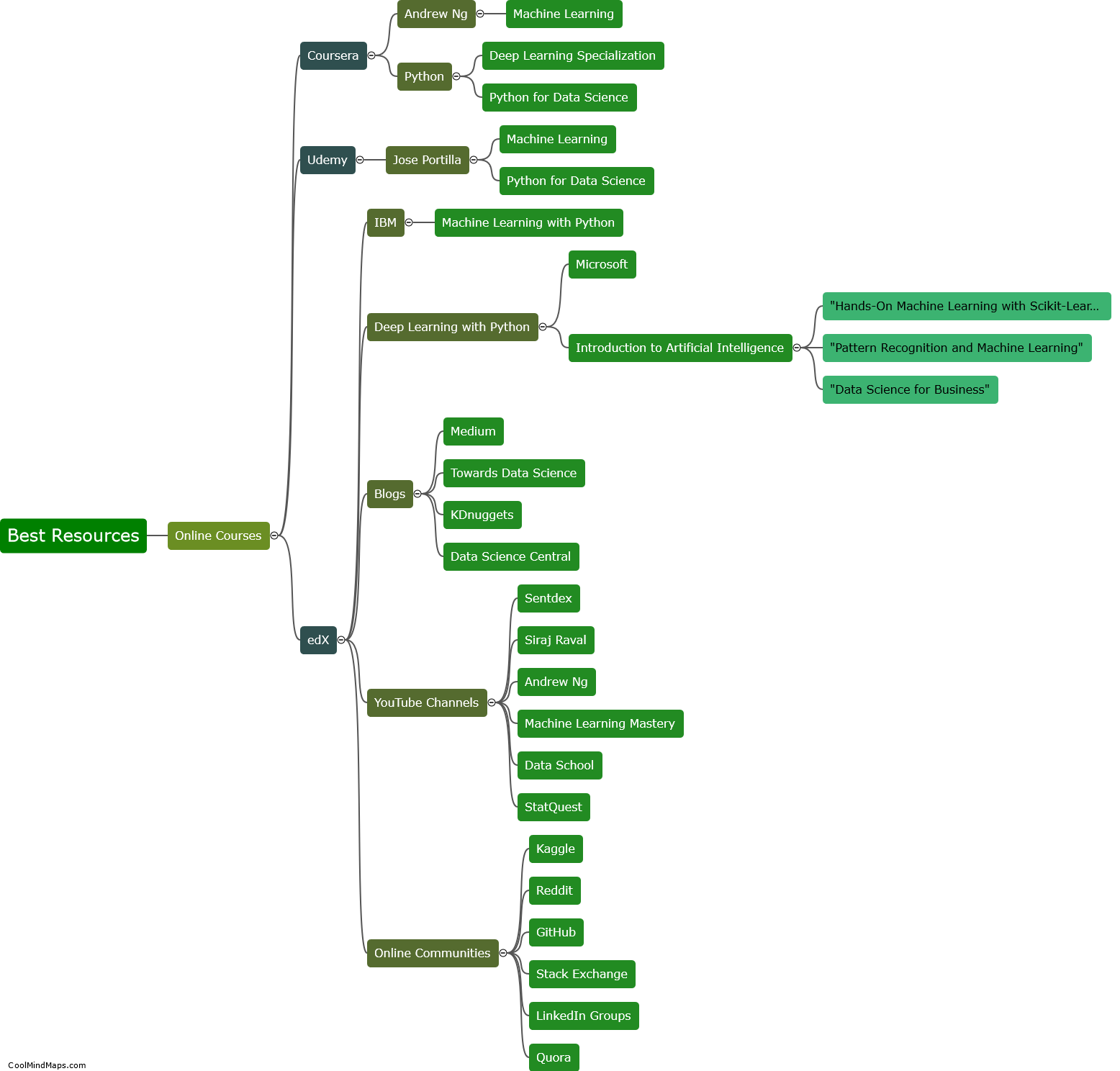
How does Riemannian geometry differ from Euclidean geometry?

Riemannian geometry and Euclidean geometry are two branches of geometry that differ in several fundamental aspects. While Euclidean geometry deals with flat, two-dimensional spaces, Riemannian geometry focuses on curved surfaces of any dimension. In Riemannian geometry, the concept of distance and angles change depending on the curvature of the surface, whereas Euclidean geometry assumes a constant curvature of zero. Riemannian geometry also introduces the concept of geodesics, which are the shortest paths between two points on curved surfaces, in contrast to the straight lines of Euclidean geometry. Additionally, Riemannian geometry incorporates the notion of a metric tensor, allowing for the measurement of distances and angles in curved spaces, providing a more flexible framework for studying the geometry of curved surfaces.

This mind map was published on 4 September 2023 and has been viewed 94 times.