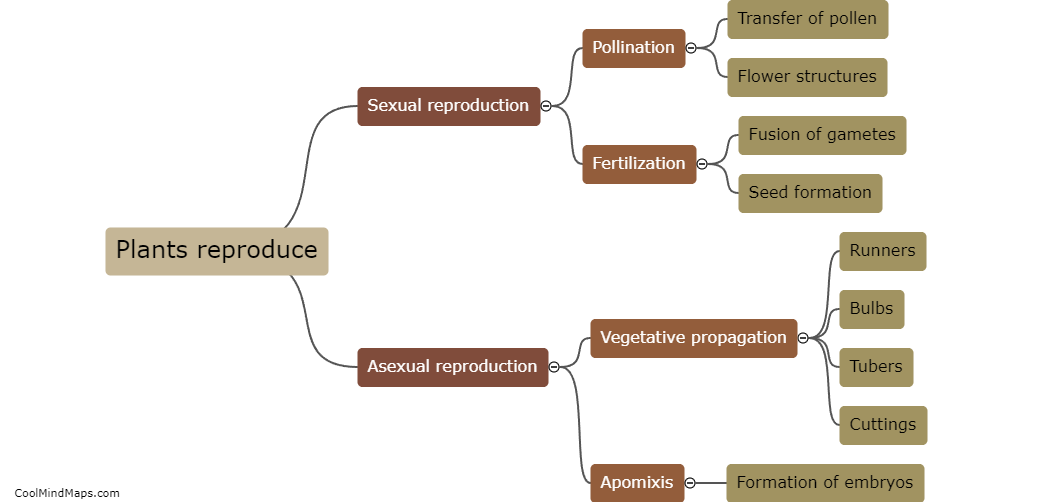
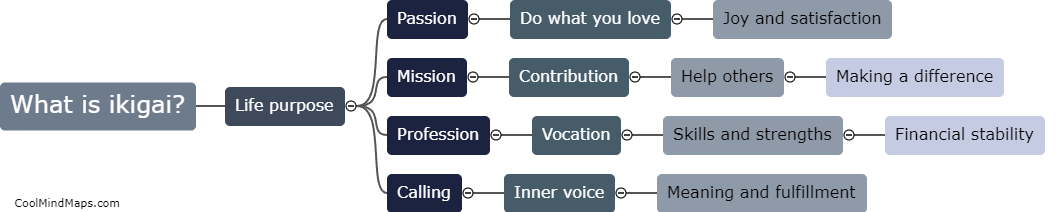
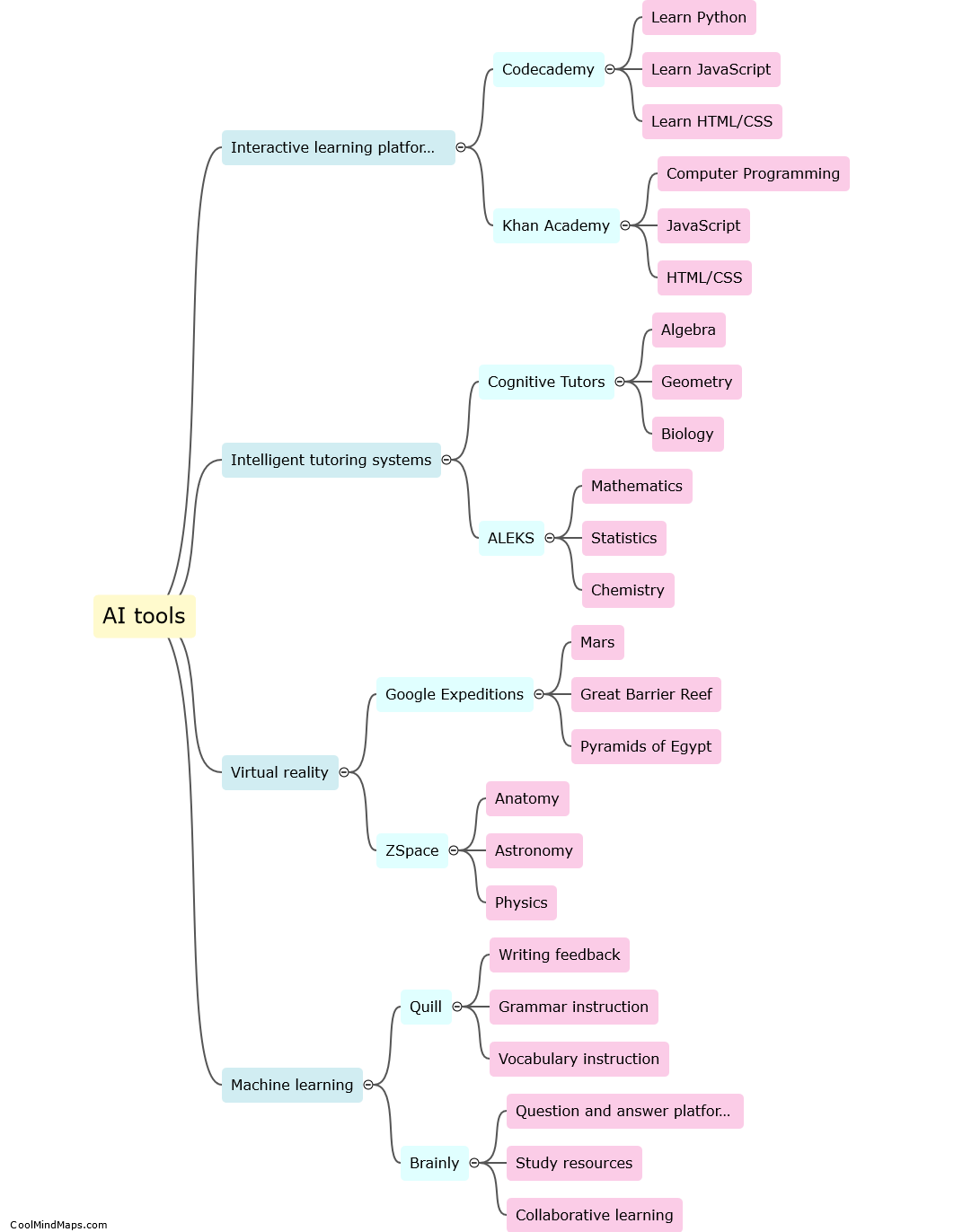
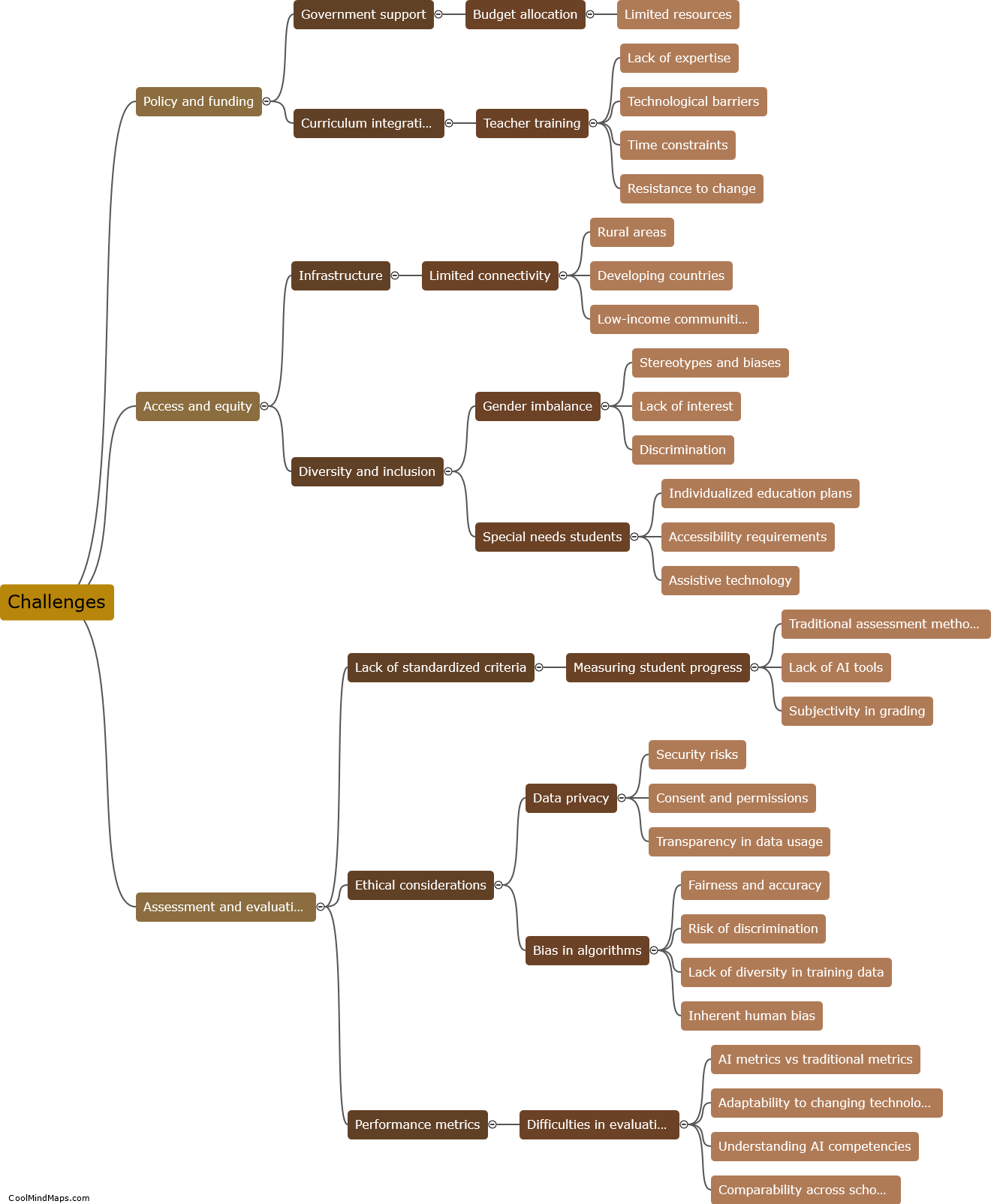
How does the graph of y = sin(x) relate to other trigonometric functions?

The graph of y = sin(x) is one of the most fundamental trigonometric functions and plays a crucial role in understanding the behavior of other trigonometric functions. It is a periodic function that oscillates between -1 and 1, forming a sine wave pattern. The graph of y = sin(x) closely resembles the graphs of other periodic trigonometric functions like y = cos(x) and y = tan(x), but with differences in phase shifts, amplitude, and period. The cosine function, for example, is shifted by 90 degrees horizontally, resulting in a wave that peaks at x = 0 instead of x = π/2. Similarly, the tangent function has vertical asymptotes and a distinct period of π. By examining the similarities and differences between the graph of y = sin(x) and other trigonometric functions, one can better understand the relationships and patterns that exist within the field of trigonometry.

This mind map was published on 29 November 2023 and has been viewed 107 times.