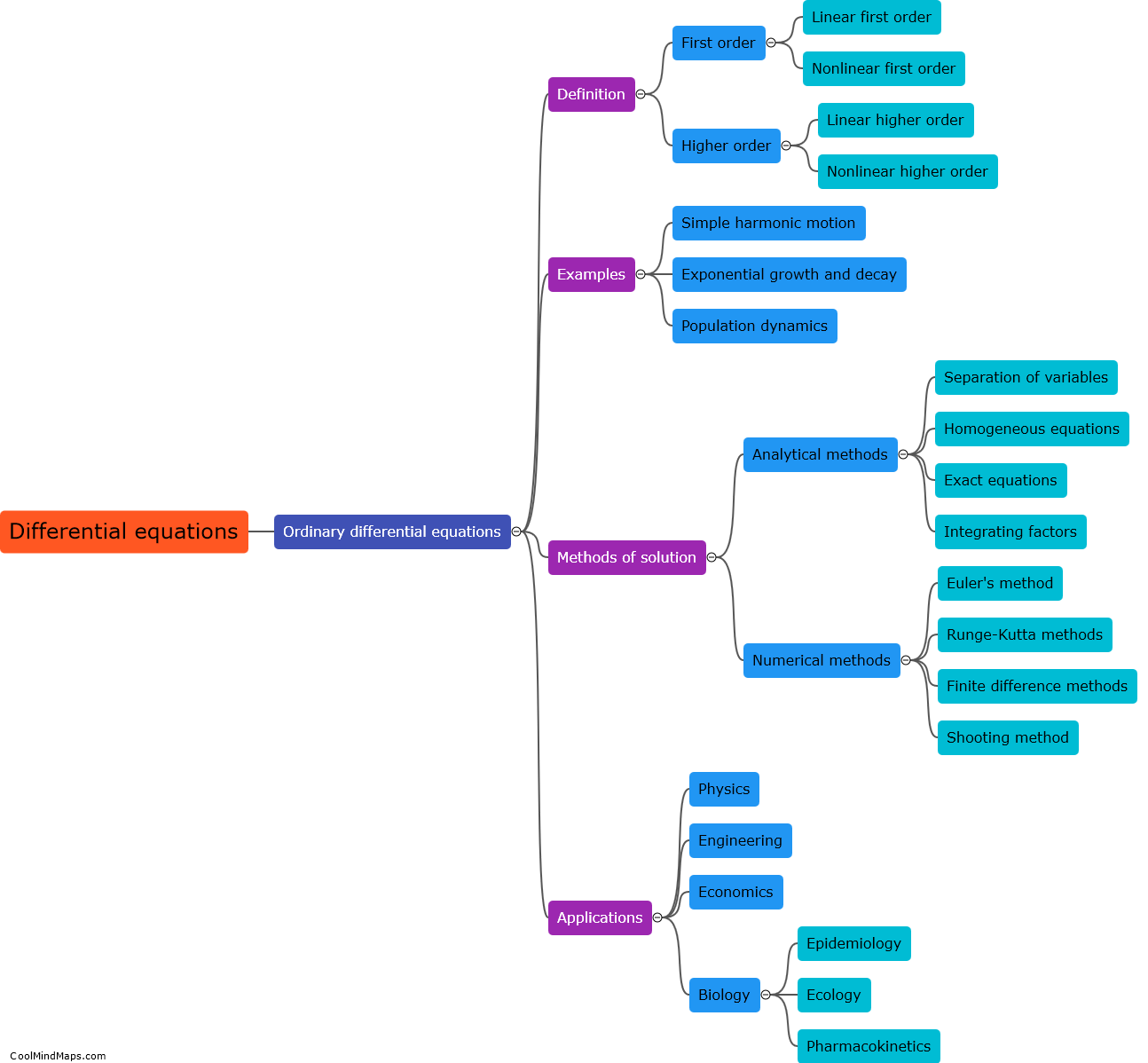
What are ordinary differential equations?

Ordinary differential equations (ODEs) are mathematical equations that involve one independent variable and one or more dependent variables and their various derivatives with respect to the independent variable. These equations describe relationships between the rates of change of the dependent variables and their values. ODEs find widespread applications in various fields of science and engineering, especially in physics and engineering disciplines. They are used to model and analyze dynamical systems, such as motion of particles, population growth, chemical reactions, and electrical circuits. The solutions to ODEs provide valuable insights into the behavior and evolution of these systems over time. Various methods and techniques, such as separation of variables, integrating factors, and numerical methods, are employed to solve ordinary differential equations.

This mind map was published on 29 November 2023 and has been viewed 103 times.