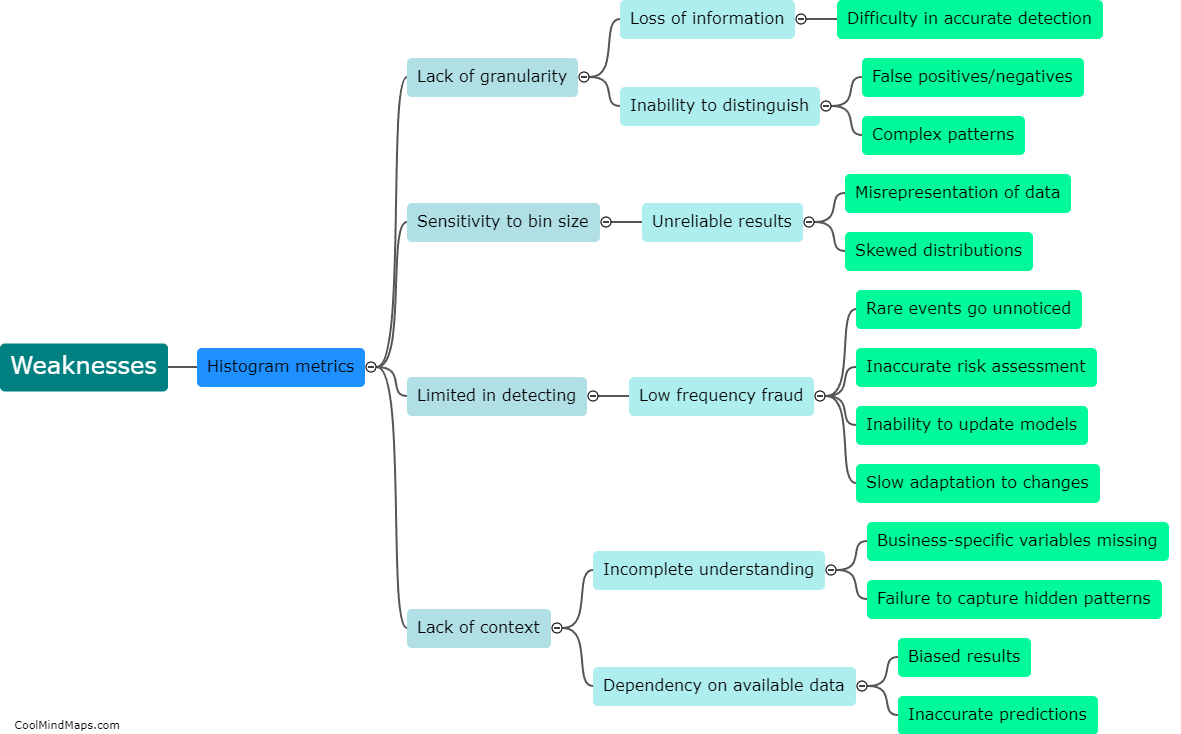
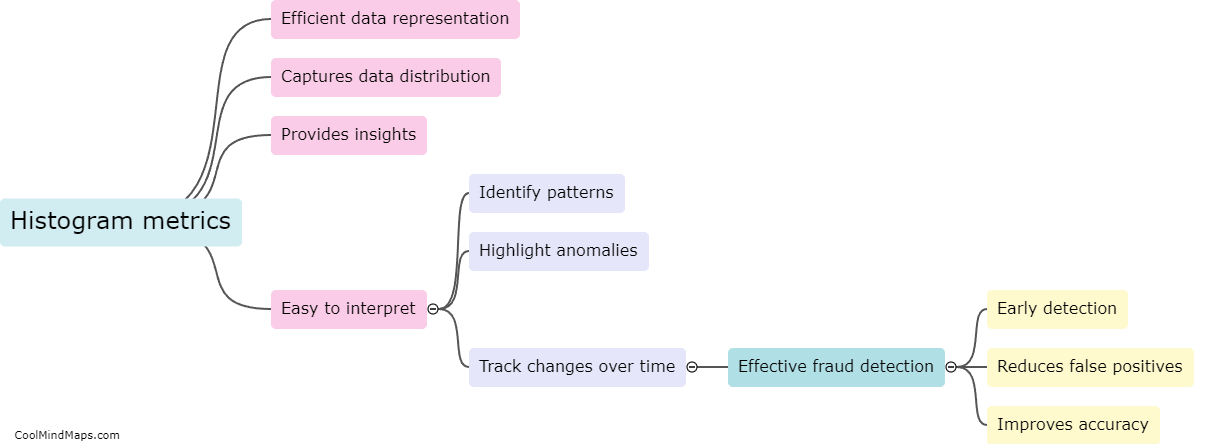
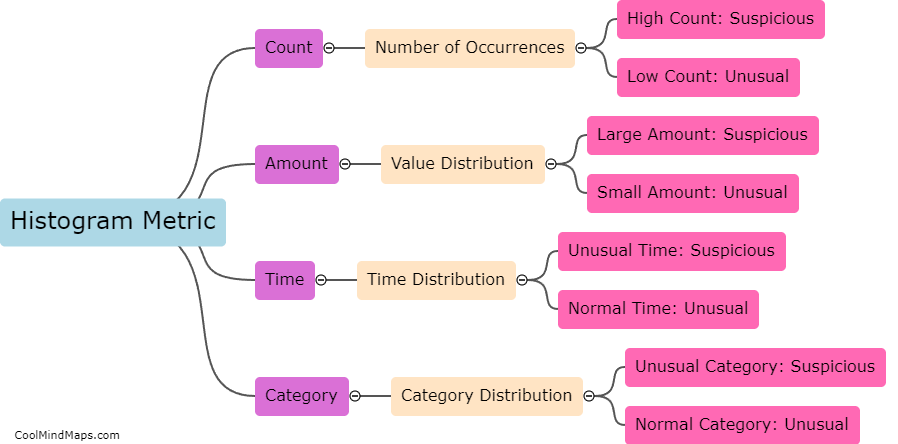
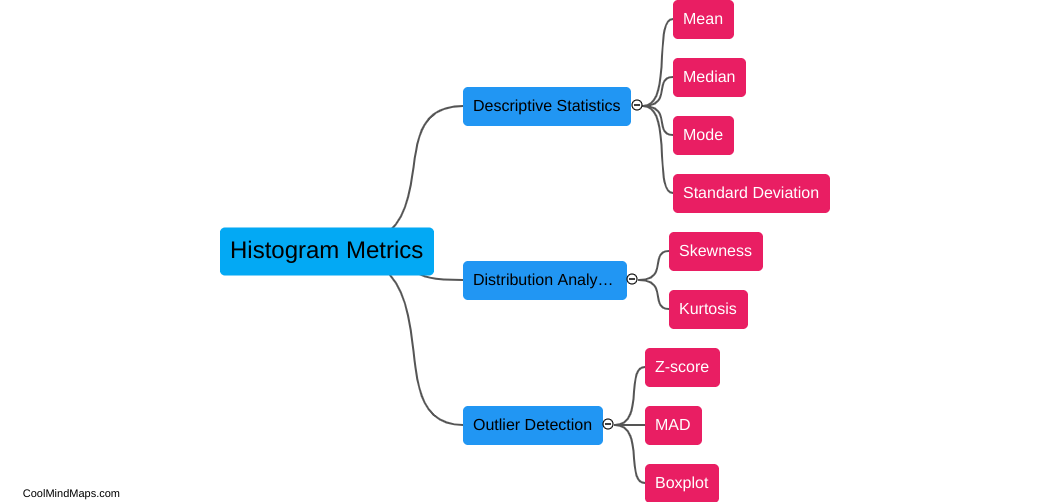
How do different types of histogram distances compare in fraud detection?

Histogram distances are common techniques used in fraud detection to measure the similarity or dissimilarity between observed data and reference distributions. Various types of histogram distances are available, and their performance can vary depending on the specific fraud detection scenario. For instance, the Euclidean distance is often used to quantify the overall distance between histograms, while the Bhattacharyya distance focuses on capturing differences in shape and spread. On the other hand, the Jensen-Shannon divergence considers both the information content and the probability distributions of the histograms. Comparing different types of histogram distances in fraud detection requires evaluating their ability to effectively capture deviations from expected patterns, detect anomalies, and provide reliable measures of similarity. Careful consideration of the specific fraud detection context and the characteristics of the data is crucial to choose the most appropriate histogram distance for a given application.

This mind map was published on 8 October 2023 and has been viewed 106 times.