What are the equations of parabolic motion?

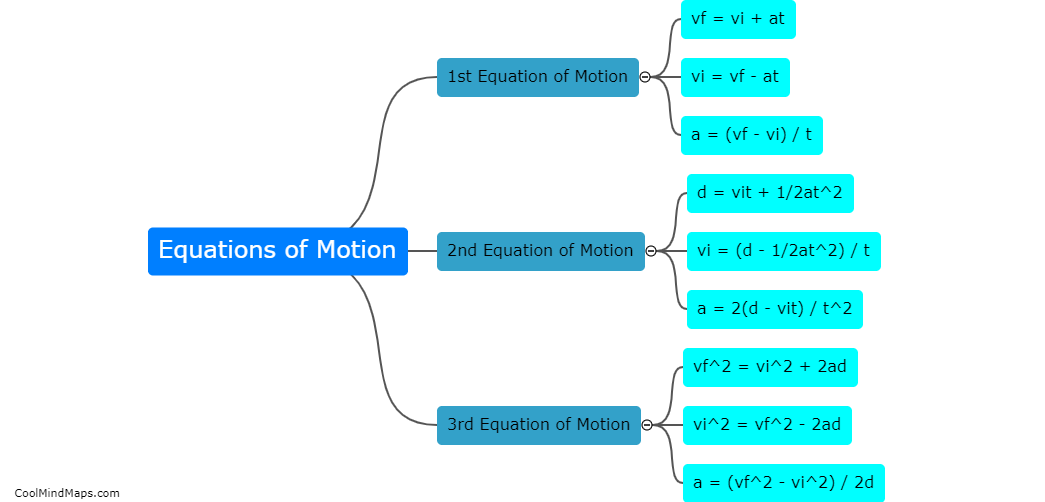
The equations of parabolic motion describe the trajectory followed by a projectile under the influence of gravity, assuming no air resistance. The motion is characterized by a parabolic path, hence the name. The equations governing this motion are derived by considering the forces acting on the object, namely, the gravitational force and any initial velocity. The vertical motion is described by the equation y = y0 + v0y*t - (1/2)gt^2, where y is the vertical position, y0 is the initial vertical position, v0y is the initial vertical velocity, g is the acceleration due to gravity, and t is the time. The horizontal motion is described by the equation x = x0 + v0x*t, where x is the horizontal position, x0 is the initial horizontal position, v0x is the initial horizontal velocity, and t is the time. These equations allow us to determine the position and velocity of a projectile at any given time during its parabolic trajectory.

This mind map was published on 5 October 2023 and has been viewed 103 times.