What are pseudometric spaces?

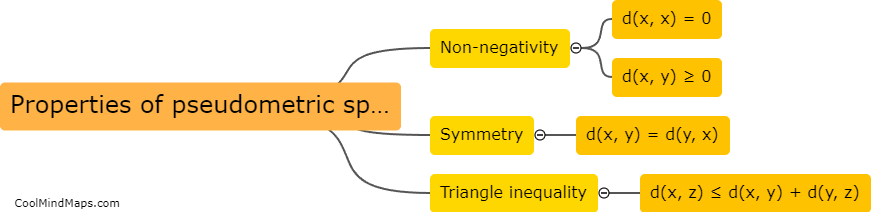
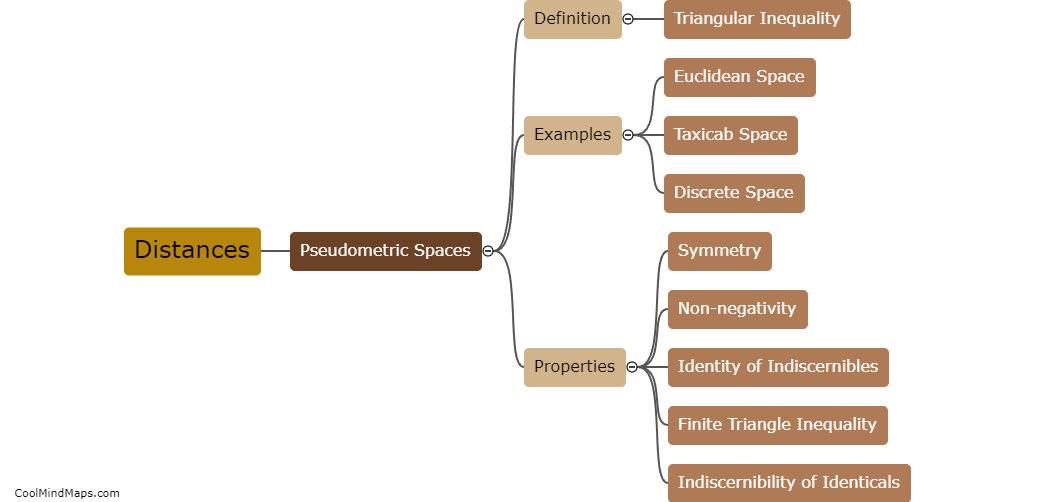
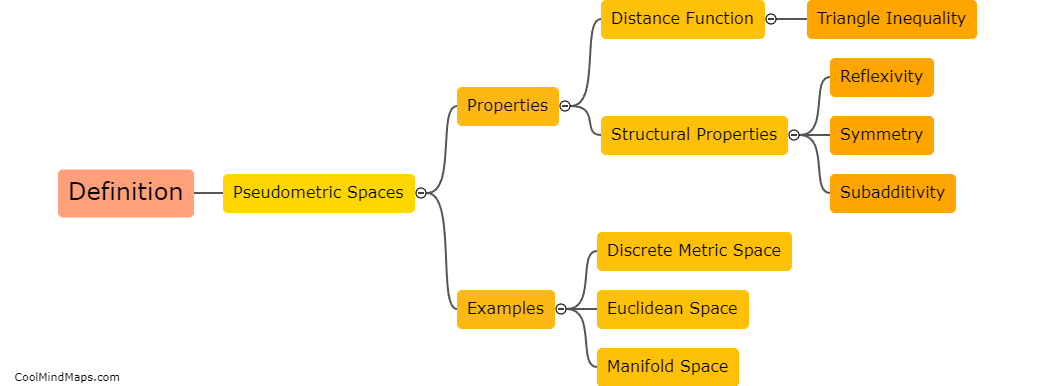
Pseudometric spaces, also known as quasi-metric spaces or semi-metric spaces, are mathematical structures that generalize the concept of distance in metric spaces. In a pseudometric space, the distance function satisfies most of the properties of a metric, such as non-negativity, symmetry, and the triangle inequality, but allows for the possibility of having a distance of zero between distinct points. This relaxation of the strict metric property allows for more flexibility in studying mathematical spaces where some points may be indistinguishable from each other. Pseudometric spaces find applications in various areas of mathematics, such as functional analysis, topology, and probability theory, providing a framework for analyzing objects that may not have well-defined distances between them.

This mind map was published on 10 November 2023 and has been viewed 115 times.