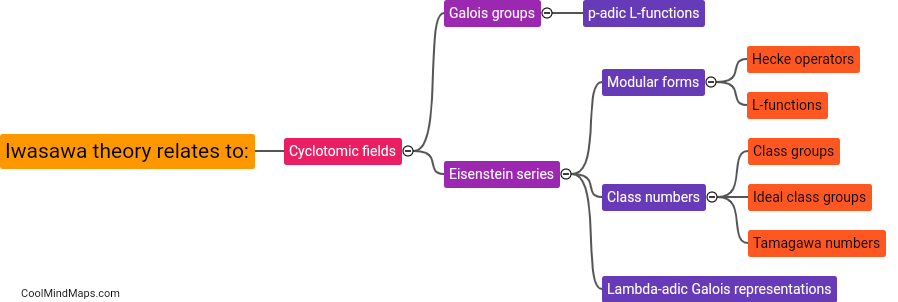
How does Iwasawa theory relate to number theory?

Iwasawa theory is a branch of number theory that explores the connection between certain algebraic objects called Galois groups and the arithmetic of number fields. Specifically, it investigates the behavior of the p-part of the class group of a number field for all primes p simultaneously. Originally introduced by Kenkichi Iwasawa in the 1950s, this theory provides a powerful tool for studying the behavior of certain arithmetic invariants in number theory, such as the class number, using concepts from algebraic number theory and algebraic geometry. The main idea behind Iwasawa theory is that there exists a fundamental relationship between arithmetic invariants and a certain infinite family of objects called p-adic L-functions. These p-adic L-functions encode deep arithmetic and geometric information and provide a bridge between arithmetic and Galois theory. Thus, Iwasawa theory has had far-reaching implications in various areas of number theory, including the study of Diophantine equations, elliptic curves, and the local-global principle.

This mind map was published on 4 September 2023 and has been viewed 62 times.