What are some applications of Riemannian geometry?

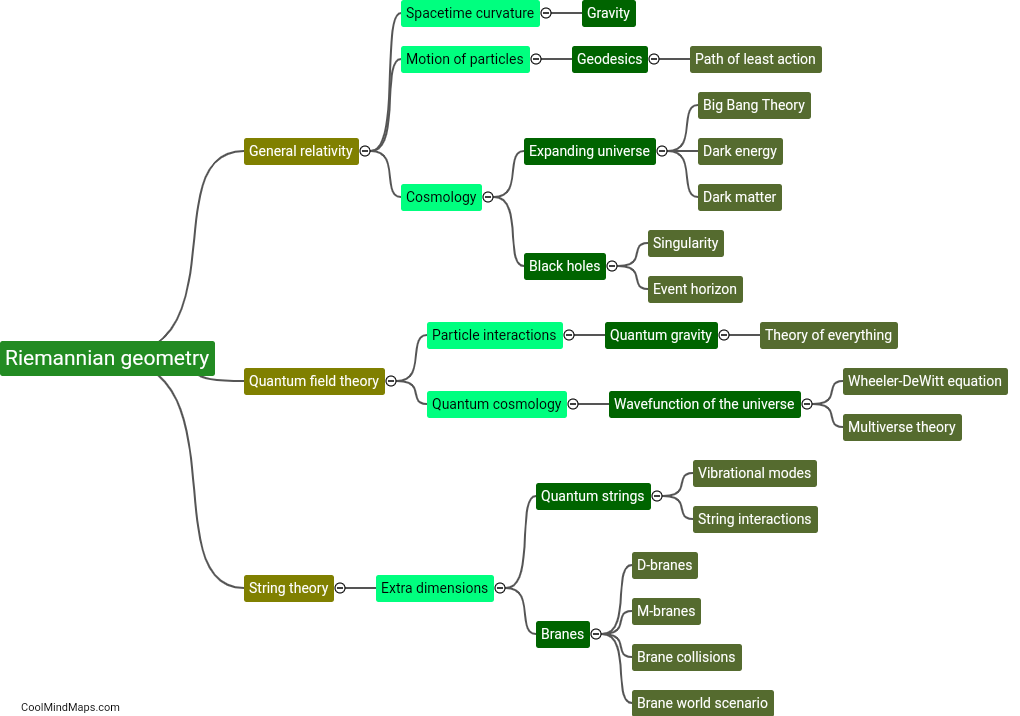
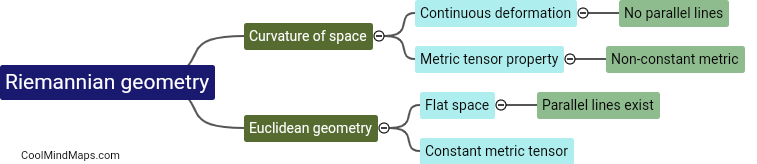
Riemannian geometry, a branch of differential geometry, has found numerous applications in various fields. One of the primary applications is in general relativity, where it serves as the geometric framework for Einstein's theory of gravity. Riemannian geometry is particularly useful in understanding the curvature of spacetime and modeling the behavior of massive objects. Additionally, this geometry has applications in computer vision, where it helps in developing algorithms for shape analysis and recognition. It also finds its utility in robotics, where it is employed to design efficient motion planning algorithms by taking into account the curvature and constraints of the robot's configuration space. Furthermore, Riemannian geometry has found applications in statistics, optimization, and machine learning, where it provides tools for analyzing high-dimensional datasets and developing efficient algorithms for optimization problems on curved manifolds. Overall, the applications of Riemannian geometry span various disciplines and play a crucial role in understanding and solving complex mathematical and real-world problems.

This mind map was published on 18 September 2023 and has been viewed 132 times.