What advantages do Fourier functions offer in determining volatility spillovers?

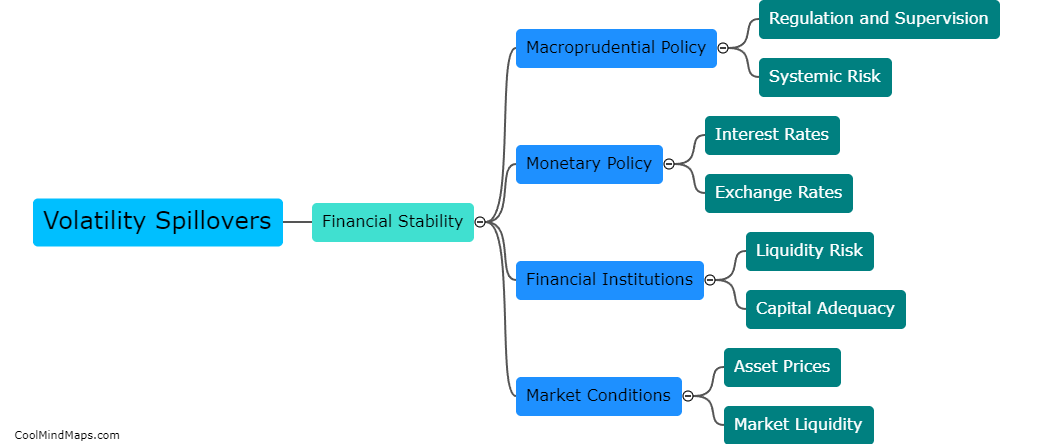
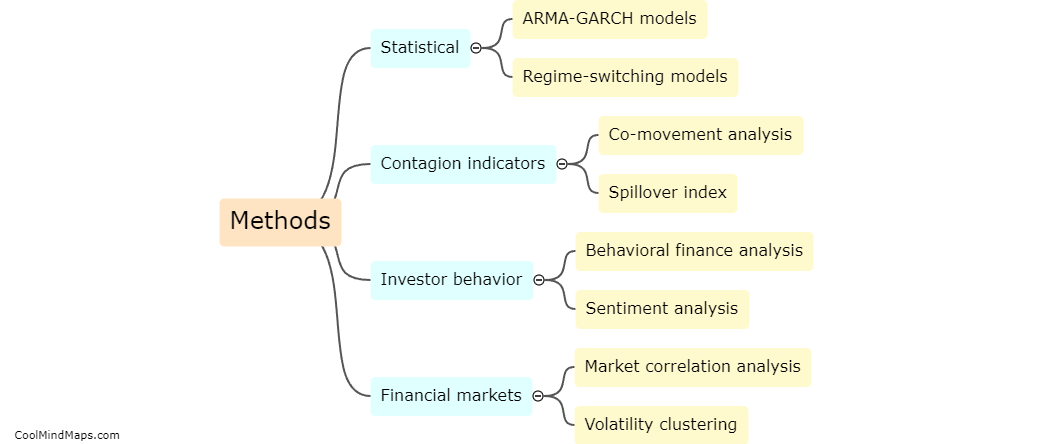
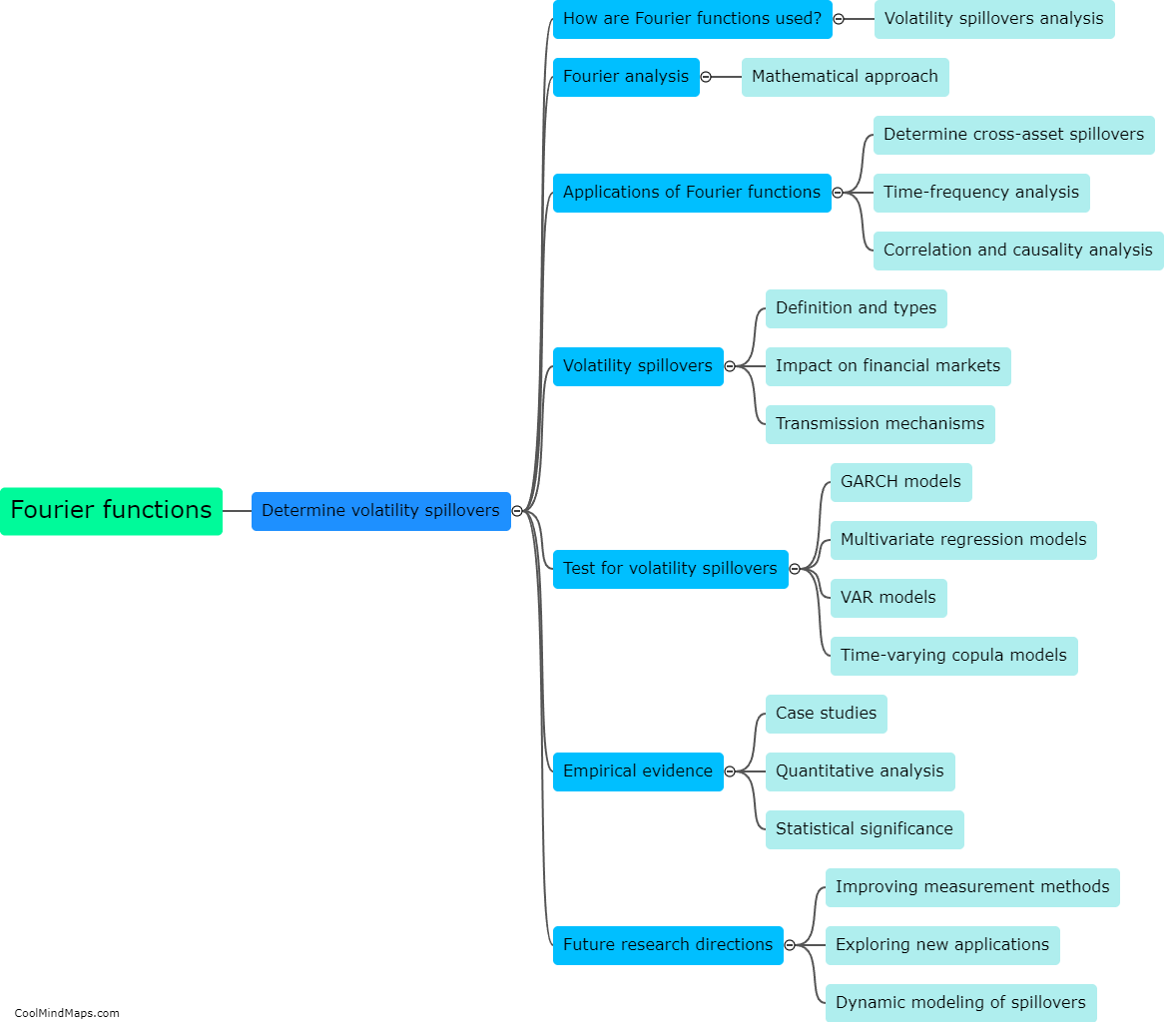
Fourier functions offer several advantages in determining volatility spillovers. Firstly, Fourier analysis allows for decomposing a time series into its constituent frequencies, enabling the identification of periodic patterns and cyclical components. This is particularly useful in studying volatility spillovers, as it helps to identify any systematic or repetitive patterns in the transmission of volatility between different markets or assets. Secondly, Fourier functions allow for a flexible and non-parametric approach to modeling volatility spillovers, by providing a continuous representation of the data without making assumptions about the functional form. This allows for capturing complex and nonlinear relationships that may exist between different variables. Lastly, Fourier functions provide a reliable tool for estimating the magnitude and direction of volatility spillovers across different frequencies, enabling researchers to assess the short-term and long-term dynamics involved. Overall, the advantages of Fourier functions make them a valuable technique in understanding and analyzing volatility spillovers.

This mind map was published on 27 November 2023 and has been viewed 93 times.