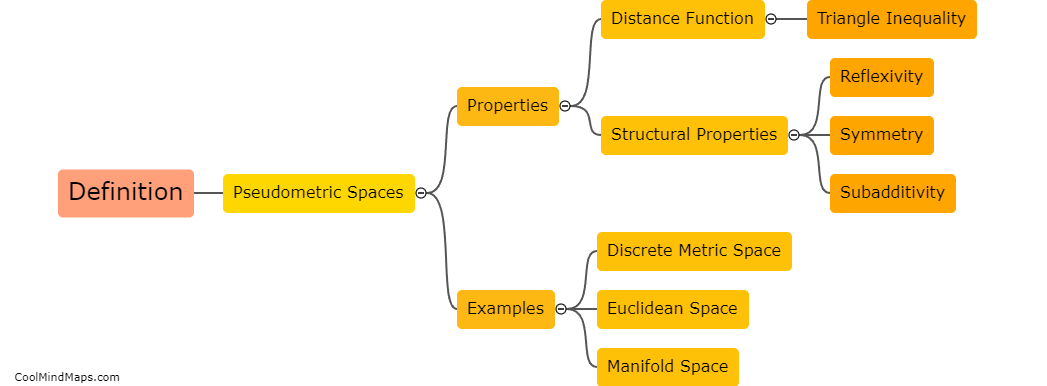
What are some examples of pseudometric spaces?

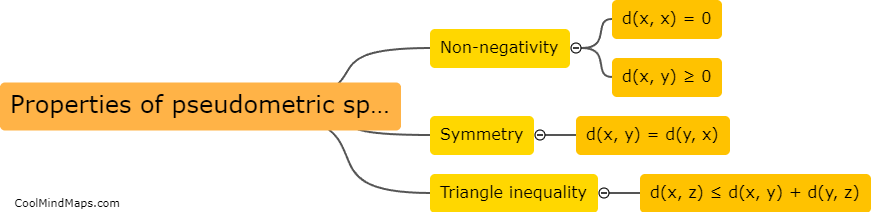
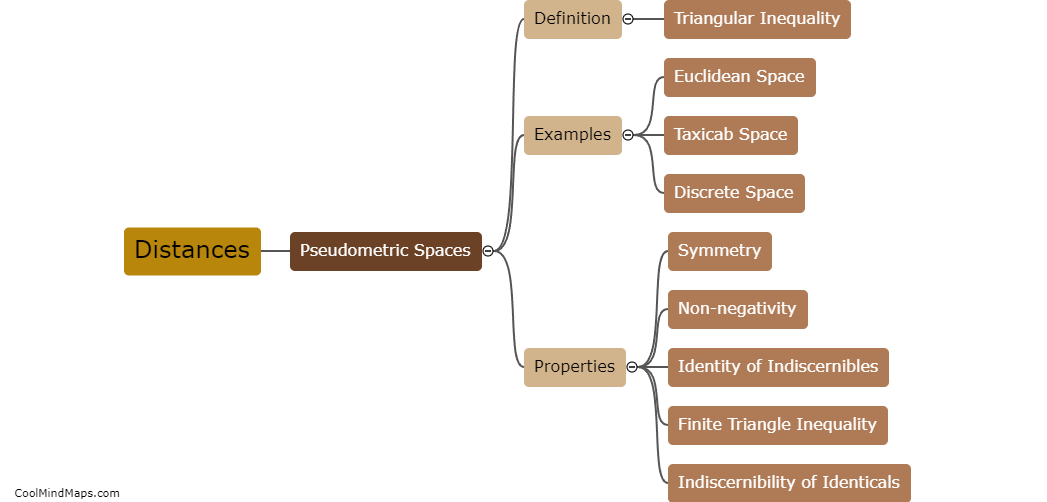
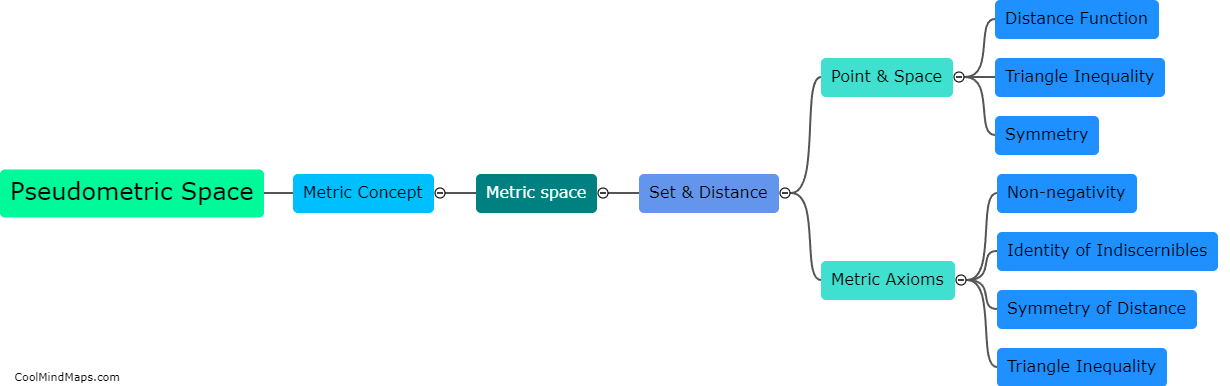
Pseudometric spaces are mathematical structures that resemble metric spaces but do not satisfy all the properties of a true metric. In a pseudometric space, the distance between two points may be zero even if the points are distinct, violating the non-negativity axiom of a metric. Some examples of pseudometric spaces include the discrete pseudometric, where the distance between any two distinct points is one, and the taxicab pseudometric, where the distance between two points is defined as the sum of the absolute differences of their coordinates. Other examples include the Minkowski pseudometric, used in geometric analysis, and the fractional pseudometric, which is a generalization of the standard metric. Pseudometric spaces provide a flexible framework for studying various mathematical concepts and can be found in many different areas of mathematics.

This mind map was published on 16 November 2023 and has been viewed 99 times.