How is a pseudometric space related to metric spaces?

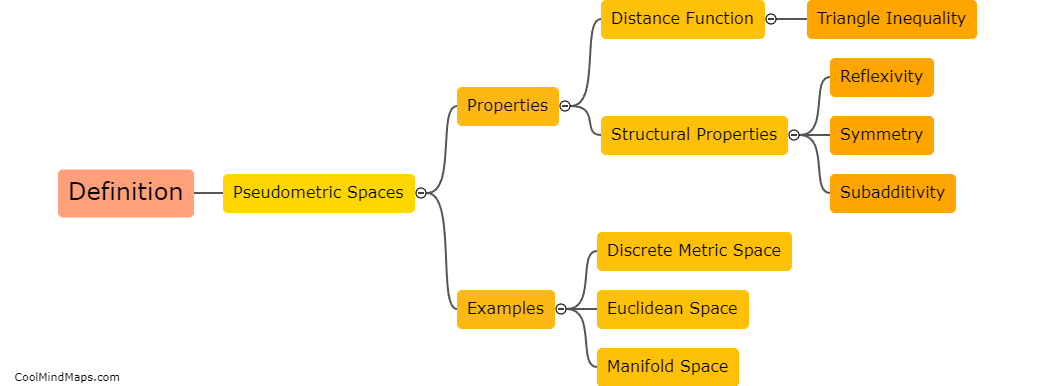
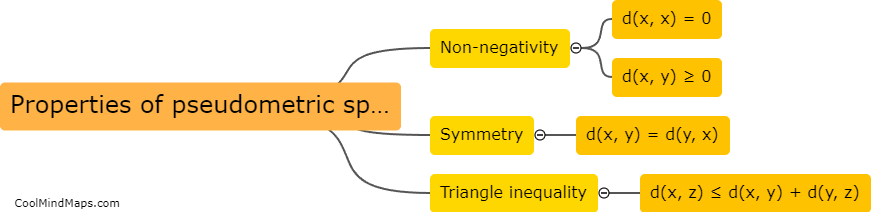
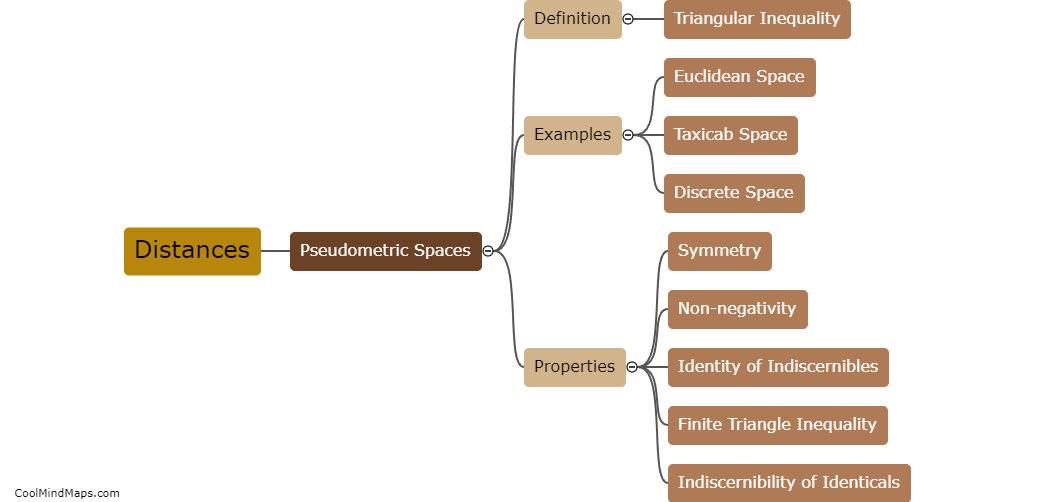
A pseudometric space is similar to a metric space, but with a more relaxed definition. While a metric space requires the distance between any two points to be non-negative, a pseudometric space allows for the distance to be zero in some cases. Additionally, a metric space must satisfy the triangle inequality (the sum of two distances is always greater than or equal to the third distance), while a pseudometric space does not necessarily need to hold this property. However, every metric space can be seen as a pseudometric space by simply disregarding the possibility of zero distances. Therefore, pseudometric spaces can be seen as a generalization of metric spaces, allowing for additional flexibility in defining distances and accommodating certain mathematical structures that may not meet all the strict requirements of a metric space.

This mind map was published on 29 November 2023 and has been viewed 104 times.